Log-Normal calculations using R
对数正太分布
R
packages
对数正态分布数据是指对数据取对数后,数据呈正态分布的数据模型。和正态分布一样,对数正态分布也有两个基本的参数:\(\sigma\) 和\(\mu\)。用R计算对数正态分布有4个基本的函数。
1 随机生成对数正态分布数据: rlnorm(n,meanlg,sdlg)
2 计算累积概率: plnorm(q,meanlg,sdlg)
3 计算临界值: qlnorm(p,meanlg,sdlg)
4 pdf值: dlnorm(x,meanlg,sdlg)
5 练习
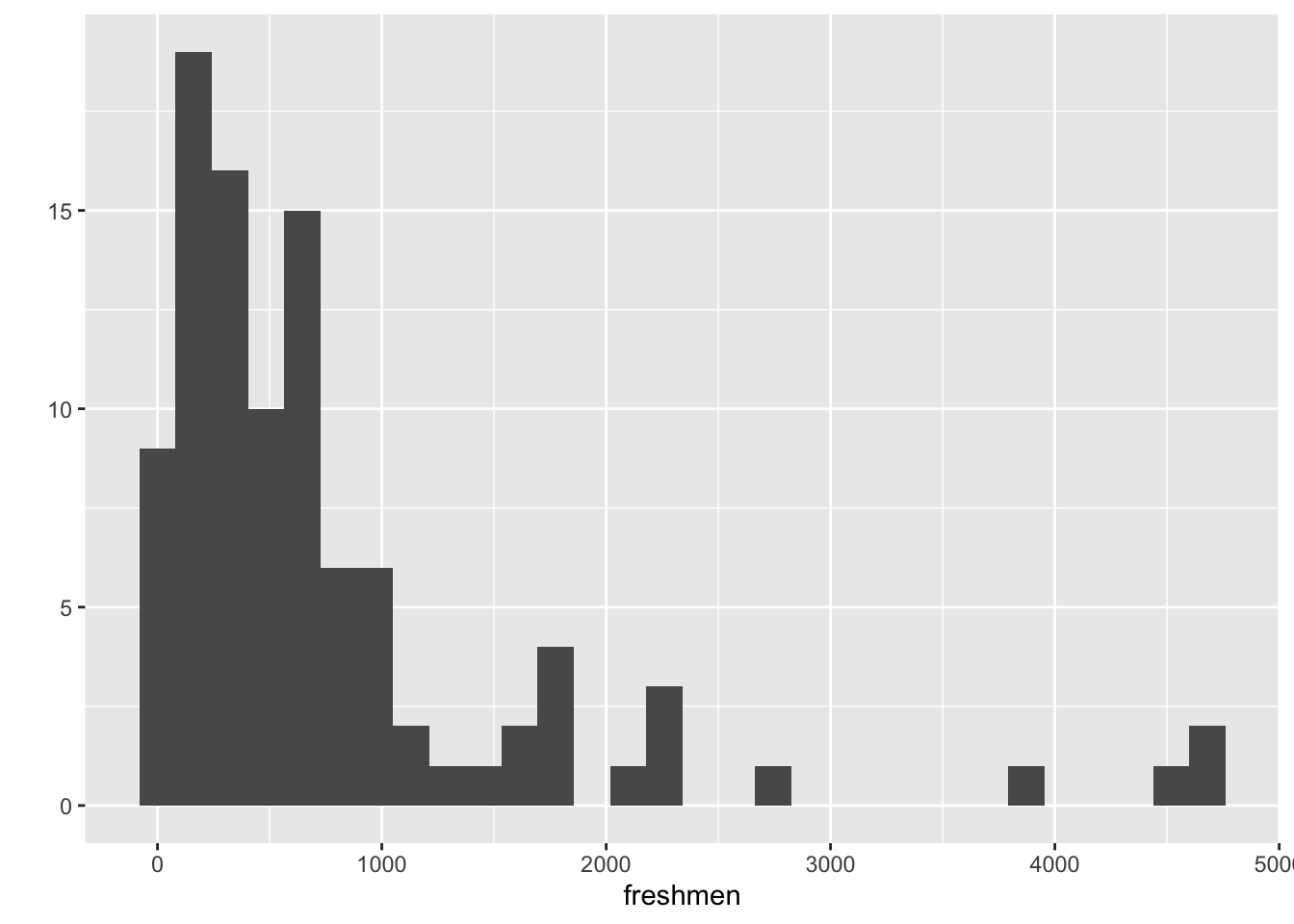
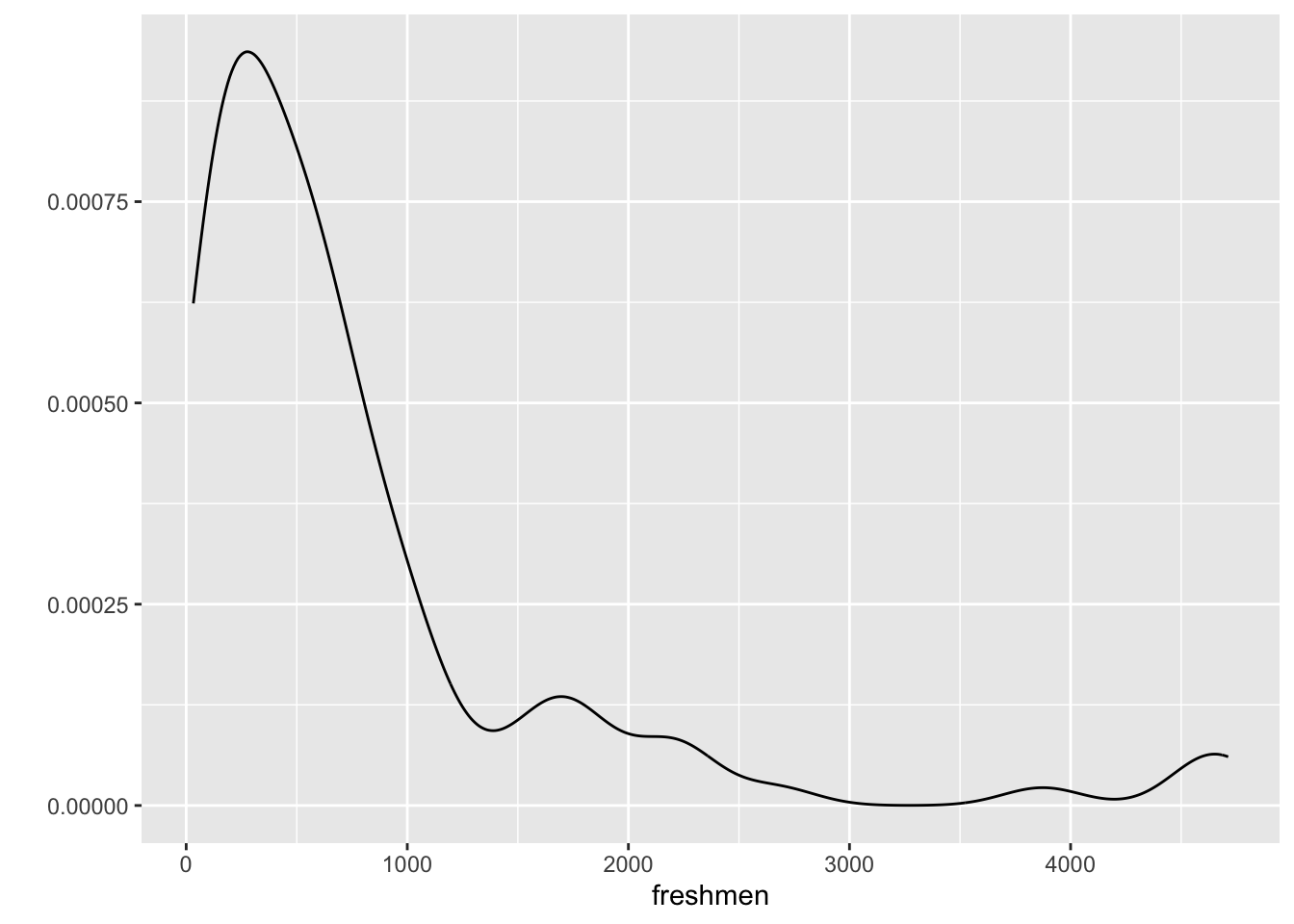
Example. Freshman undergraduate enrollments at U.S. colleges have an approximate log-normal distribution with parameters mean = 6.1 and sd = 1.0. ### What is the probability that a randomly-selected college enrolls between 500 and 1000 freshmen in a year?